Lower Bounds for Geometric Algorithms

\(\DeclareMathOperator{\cut}{\text{cut}} \DeclareMathOperator{\maxcut}{\text{Max-Cut}} \DeclareMathOperator{\E}{\mathbb{E}} \DeclareMathOperator{\poly}{\mathrm{poly}} \DeclareMathOperator{\diam}{\mathrm{diam}} \DeclareMathOperator{\polylog}{\poly \log} \DeclareMathOperator{\Unif}{\mathrm{Unif}} \DeclareMathOperator{\TVD}{\text{TVD}}\)

In my last post, I defined the dynamic (or turnstile) streaming model. There is a related but weaker model called insertion-only (or vanilla) streams where deletions are forbidden. Though it sounds weird, but it is rare when for some problems there are seperations between two models. Indeed, in common streaming algorithms, the most frequent primitives people use are sampling, maintaining some sums, or doing these after some hashing. All of them can be performed in dynamic streams.

Can we seperate them then? Well, there is a simple geometric problem getting attention in the folklore. For a bounded subset $P \subset \mathbb R^d$, we can define its diameter $\diam(P) := \sup_{x,y \in P} d(x,y)$. Now consider the problem to approximate the diameter of the input streams within a constant ratio. This problem is very simple in insertion-only streams because one can compute $\max_{x \in P} d(x,P_1)$ where $P_1$ is the first point in the stream. Think for a moment and one can see that this is a $2$-approximation.

But things get more complicated in dynamic streams. You cannot store a point, and then compute its distances with others. This can be explained by a powerful theorem characterizing dynamic streaming algorithms as linear sketches.

Theorem (Linear Sketches Are Optimal). ¹² Suppose there is a universe $[N]$ and a decisional problem computing a set function $f:\lbrace 0,1\rbrace^{[N]} \to \lbrace 0,1\rbrace$. Any dynamic streaming algorithms solving this problem in $S$ bits space with constant probability can be implemented by a probabilistic linear map $\mathbb Z^n \to \mathbb Z_{q_1}\otimes \cdots \mathbb Z_{q_{\tilde O(S)}}$ ($q$ is also stochastic) supported on $\tilde O(n)$ matrices with integer entries bounded by $\poly(n)$. The theorem also holds for relational problems or general vectors instead of sets.

The theorem implies that the algorithm must be “oblivious” to each point. Even though, there exists an algorithm with $O\left(n^{\varepsilon^2}\right)$ space for $O(1/\varepsilon)$-approximation. TODO. Hint: JL

Now we aim for a matching exponential lower bound. We construct a hard instance where the algorithm must distinguish between two cases.

1. Draw $v\sim N(0,I_d/d)$. Draw $n$ i.i.d. vectors $v_1,\ldots,v_{n-1}$ from $v+\varepsilon N(0,I_d/d)$. Let $P={v_1,\ldots,v_{n-1},v_n:=v}$. Then $\diam(P) \approx \varepsilon$
2. Similar as Case 1, but replace $v_n$ with $-v$. Then $\diam(P) \approx 2-\varepsilon$.

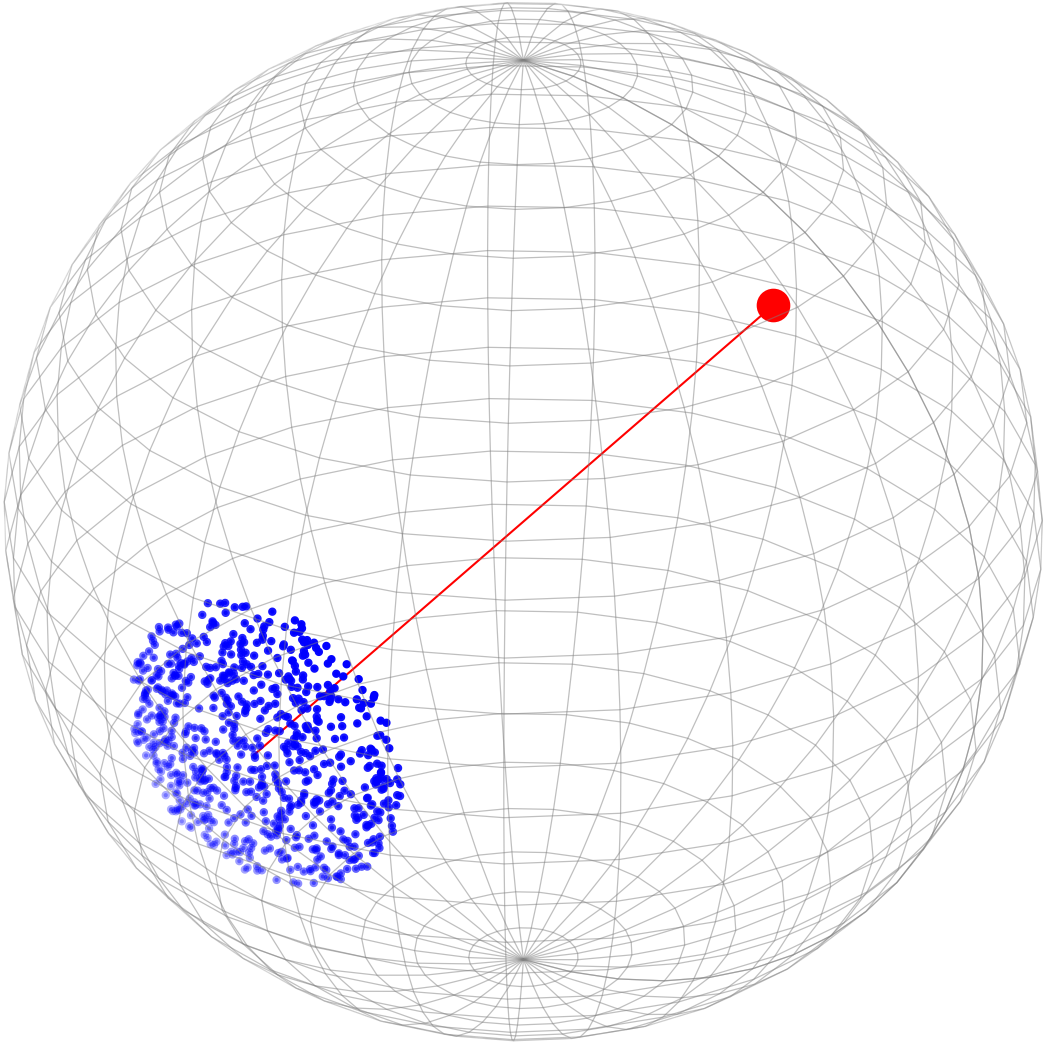
We should point out that, the figure is misleading, because $\varepsilon$-spherical cap should occupy $1 - \exp(-cd\varepsilon^2)$ fraction of the sphere³.

By the linear sketches theorem and Yao’s minimax principle, we can model the streaming algorithm as a map $\varphi : \mathbb R^n \to G$ for some finite abelian group $G$. Denote $A := \sum_{i \le n} \varphi(v_i)$ and $B = A + (\varphi(-v) - \varphi(v))$. We want to prove that $A \approx_{\TVD} B$, where $\TVD$ stands for the total variation distance.